二次函数思维导图,思维导图模板知识点详细整理
发布时间: 2024-1-23 | 标签:二次函数 二次函数思维导图 思维导图
最近很多朋友在找二次函数思维导图,二次函数是数学中的重要概念,它描述了一个变量与另一个变量的关系的曲线形状。在许多实际应用中,如物理学、工程学和经济学等,都需要用到二次函数的知识。因此,掌握二次函数的知识对于理解和解决实际问题非常重要。本文将详细整理二次函数思维导图模板和知识点,帮助你更好地理解和掌握这一概念。

概念
二次函数是指形式为y=ax^2+bx+c的函数,其中a、b、c为常数,且a≠0。它是未知数的最高次数为二次的多项式函数,图像为抛物线。根据a的符号,抛物线有不同的开口方向,a>0时开口向上,a<0时开口向下。顶点坐标为(-b/2a, c-b^2/4a),对称轴为x=-b/2a。
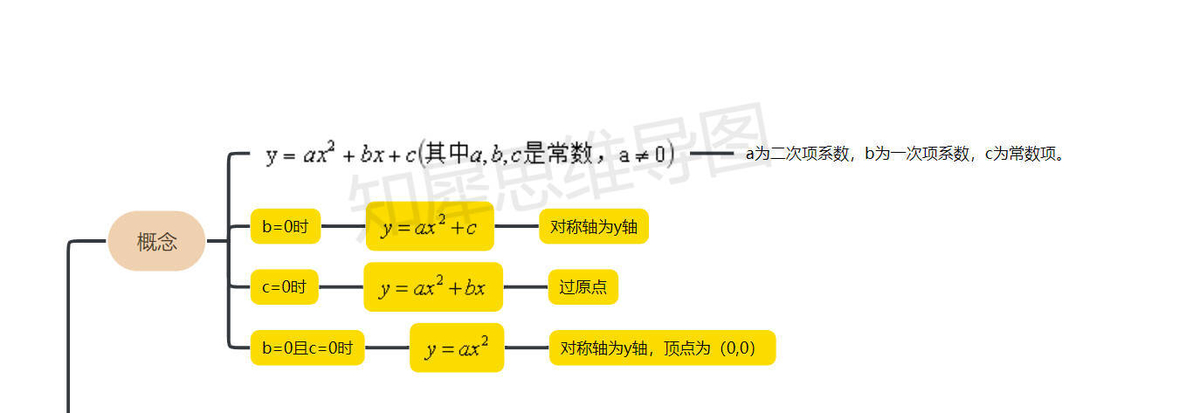
表达式
二次函数的表达式为y=ax^2+bx+c,其中a、b、c为常数,且a≠0。这个表达式可以用来描述一个变量y与另一个变量x之间的二次关系。当a>0时,函数图像开口向上,当a<0时,函数图像开口向下。对称轴为x=-b/2a,顶点坐标为(-b/2a, c-b^2/4a)。根据判别式Δ=b^2-4ac的值,可以判断方程的实根个数。当Δ>0时,有两个不相等的实根;当Δ=0时,有两个相等的实根;当Δ<0时,无实根。

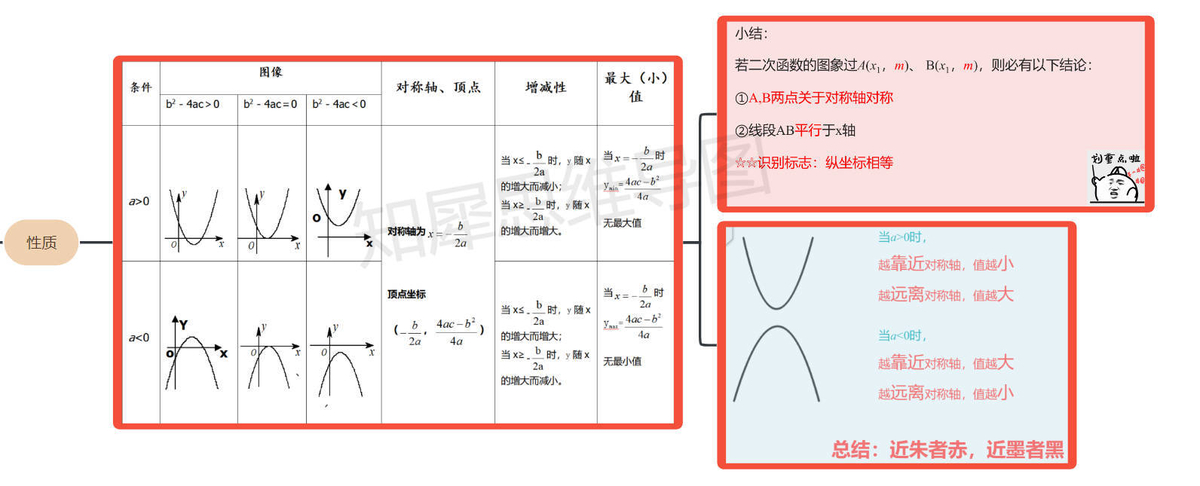
图像

性质
首先明确二次函数的定义,即形式为y=ax^2+bx+c的函数,其中a、b、c为常数,且a≠0。
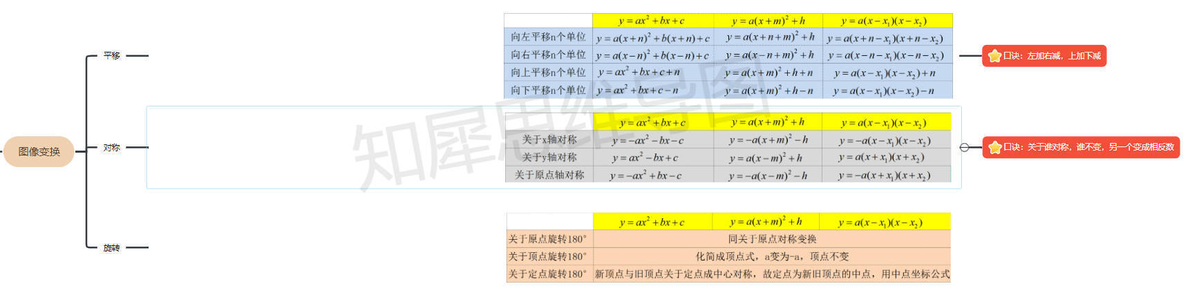
图像变换
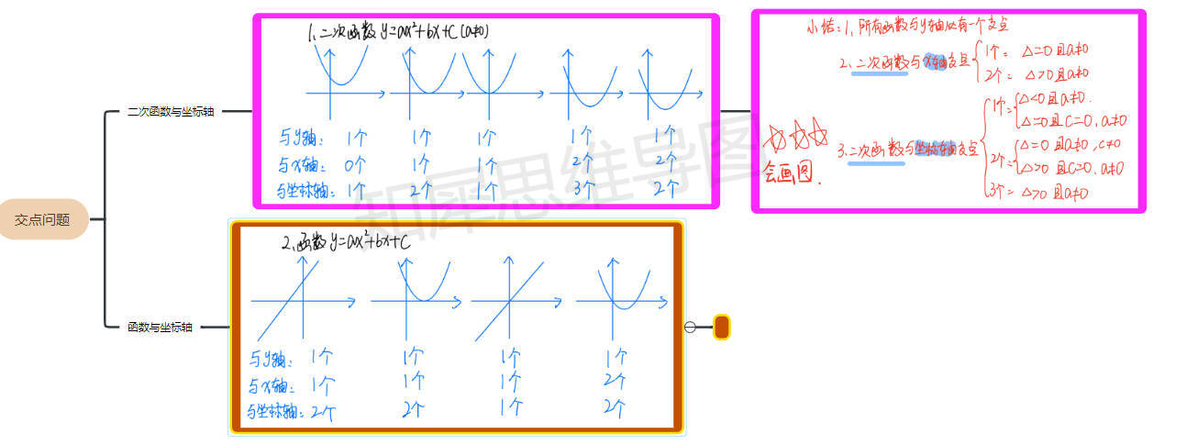
与X轴交点

交点问题
二次函数与Y轴始终有交点(当x=0时,y必有一个值)。这个交点的纵坐标的值就是函数表达式中c的值。
abc的符号对抛物线形状位置的影响

截距公式

八年级数学下册二次函数
T10
函数三要素求解
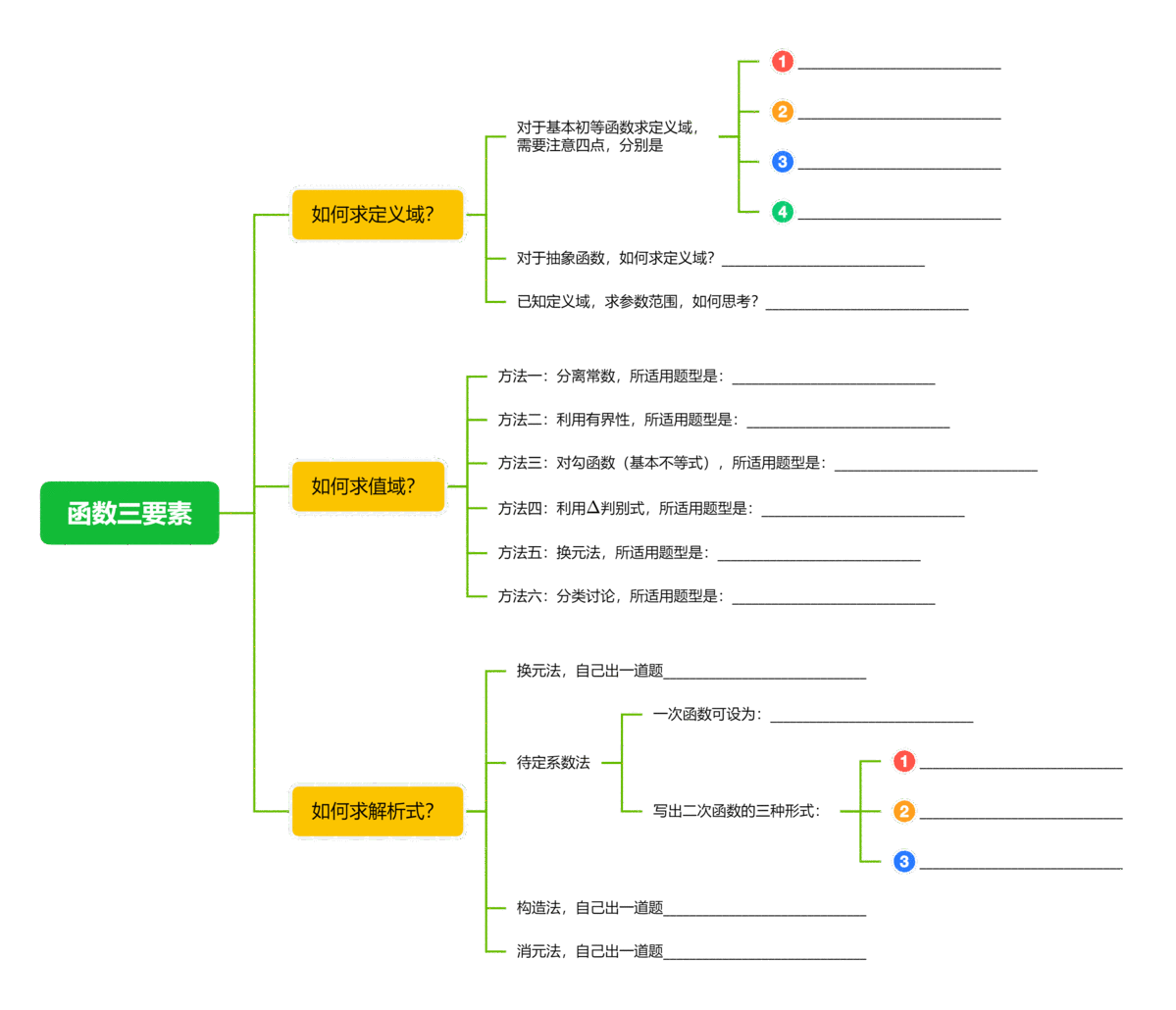
以上就是二次函数思维导图,我们对二次函数有了更深入的理解。作为数学中的重要概念,二次函数在解决实际问题中有着广泛的应用。掌握二次函数的知识,对于提高我们的数学素养和解决实际问题的能力都具有重要意义。希望本文能对大家的学习有所帮助,也希望大家能够继续深入学习和探索二次函数的奥秘。
关键词:二次函数思维导图,二次函数,思维导图,数学思维导图

